线代本质#5:点积(数量积)叉积(向量积)与其几何理解(向量点积、叉积) 作者: bluish 时间: 2025-06-30 分类: 未分类 #点积(数量积) 点积的几何含义为: **向量m于向量n上的投影,乘以向量n的长度的值。**两者的逻辑顺序可调换,投影乘法与顺序无关。 故公式A:<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mrow><mover><mi>m</mi><mo stretchy="false">→</mo></mover></mrow><mo data-mjx-texclass="CLOSE">|</mo></mrow><mo>⋅</mo><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mrow><mover><mi>n</mi><mo stretchy="false">→</mo></mover></mrow><mo data-mjx-texclass="CLOSE">|</mo></mrow><mo>⋅</mo><mi>cos</mi><mo data-mjx-texclass="NONE"></mo><mi>θ</mi></math> 此外,存在等价公式B(设两向量为(x1,x2)(y1,y2)): <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msub><mi>x</mi><mrow><mn>1</mn></mrow></msub><msub><mi>x</mi><mrow><mn>2</mn></mrow></msub><mo>+</mo><msub><mi>y</mi><mrow><mn>1</mn></mrow></msub><msub><mi>y</mi><mrow><mn>2</mn></mrow></msub></math> ##相等原因 **向量m于向量n上的投影,可看作是一个矩阵变换。** 1. 因矩阵变换完全由基向量决定,所以做单位基向量ihat、jhat与n的投影。 2. 可见,ihat于单位向量u上的投影长度即为u的横坐标ux,jhat同理。故变换矩阵为[ux uy]。 3. 因向量m为基向量的线性组合,所以向量m经投影变换后的数值为:x1ux+y1uy 4. n向量的长度等于其与u的坐标比例,即x2/ux=y2/uy=|n|,故点积为: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mo stretchy="false">(</mo><msub><mi>x</mi><mrow><mn>1</mn></mrow></msub><msub><mi>u</mi><mrow><mi>x</mi></mrow></msub><mo>+</mo><msub><mi>y</mi><mrow><mn>1</mn></mrow></msub><msub><mi>u</mi><mrow><mi>y</mi></mrow></msub><mo stretchy="false">)</mo><mo>×</mo><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mi>n</mi><mo data-mjx-texclass="CLOSE">|</mo></mrow><mo>=</mo><msub><mi>x</mi><mrow><mn>1</mn></mrow></msub><msub><mi>u</mi><mrow><mi>x</mi></mrow></msub><mfrac><msub><mi>x</mi><mrow><mn>2</mn></mrow></msub><msub><mi>u</mi><mrow><mi>x</mi></mrow></msub></mfrac><mo>+</mo><msub><mi>y</mi><mrow><mn>1</mn></mrow></msub><msub><mi>u</mi><mrow><mi>y</mi></mrow></msub><mfrac><msub><mi>y</mi><mrow><mn>2</mn></mrow></msub><msub><mi>u</mi><mrow><mi>y</mi></mrow></msub></mfrac><mo>=</mo><msub><mi>x</mi><mrow><mn>1</mn></mrow></msub><msub><mi>x</mi><mrow><mn>2</mn></mrow></msub><mo>+</mo><msub><mi>y</mi><mrow><mn>1</mn></mrow></msub><msub><mi>y</mi><mrow><mn>2</mn></mrow></msub></math> 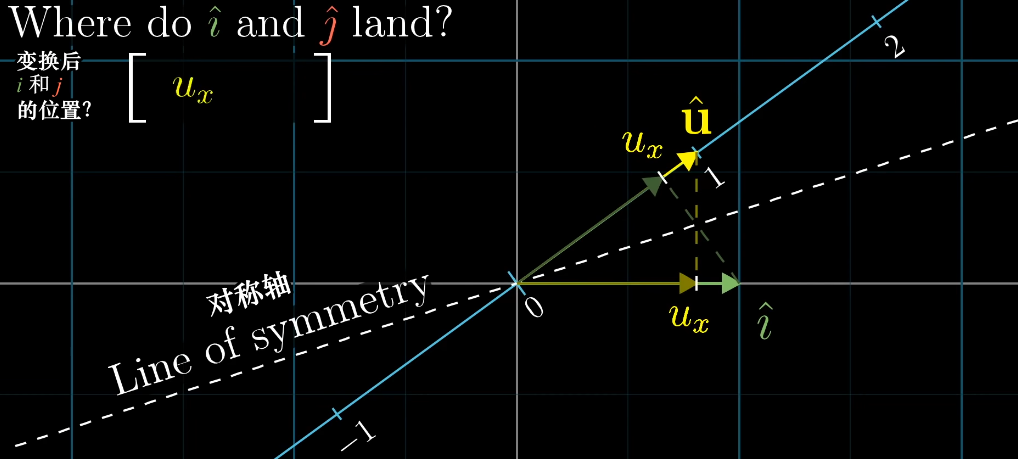 #叉积(向量积) 点积的结果为一个值,叉积的结果为一个向量,但叉积的行列式值也具备重要意义。 叉积的向量: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mi>c</mi><mo>=</mo><mi>a</mi><mo>×</mo><mi>b</mi><mo>(形式定义)</mo></math> 叉积的模: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mo stretchy="false">|</mo><mi>c</mi><mrow><mo stretchy="false">|</mo></mrow><mo>=</mo><mrow><mo stretchy="false">|</mo></mrow><mi>a</mi><mrow><mo stretchy="false">|</mo></mrow><mo>⋅</mo><mrow><mo stretchy="false">|</mo></mrow><mi>b</mi><mrow><mo stretchy="false">|</mo></mrow><mo>⋅</mo><mi>sin</mi><mo data-mjx-texclass="NONE"></mo><mi>θ</mi></math> ##叉积的意义 叉积c的意义:供给计算——任意一个向量与空间中已给定的v、w向量构成的平行六面体的体积;此外,它的模自身也代表v、w构成的平行四边形面积。 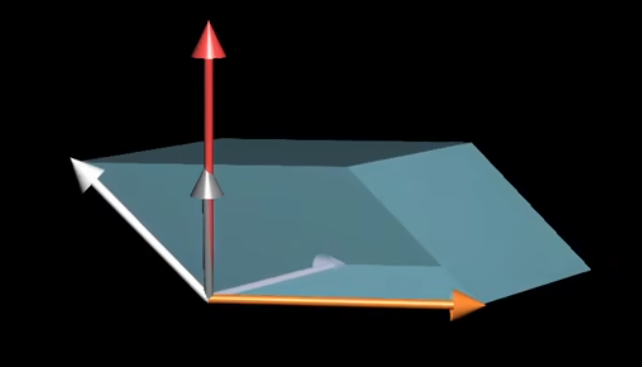 1. 已给定的v、w向量构成平行四边形 2. 平行六面体的面积为底面积(v、w平行四边形)×高度 3. 叉积向量与v、w均垂直,并且模为平行四边形的面积; **故第三向量于叉积c上的投影,乘以叉积的模,即为平行六面体的体积。** 因此叉积需满足:叉积的模为向量v、w构成平行四边形的面积;叉积的模与第三向量的点积为平行六面体的体积。 叉积c所需满足公式: 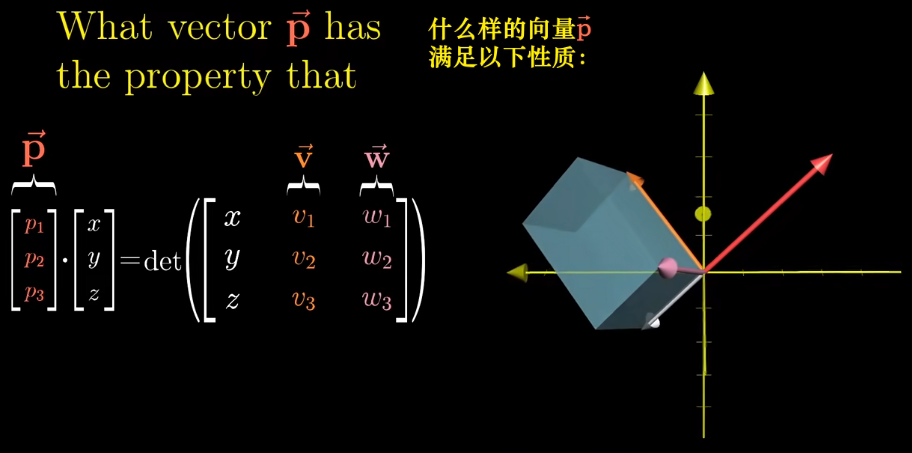 此行列式代表着——第三向量于叉积上的投影乘以叉积的模(即v、w平行四边形的面积),等于由v、w和第三向量组成的平行六面体的体积。右侧式中第一、二、三列分别代表六面体的三边)。因v、w均确定,所以叉积c也为确定值(方向、模已确定)。 ##叉积的计算 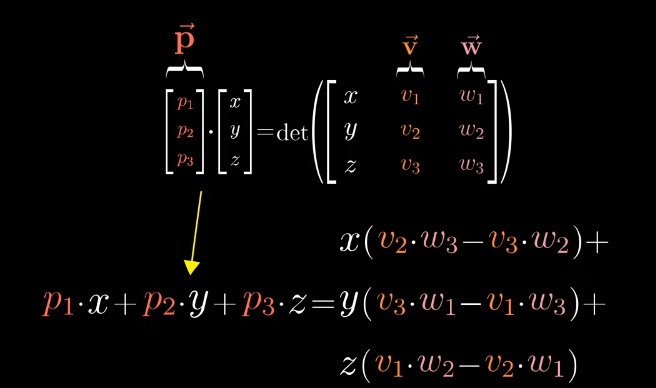 化解此公式,提取系数,得叉积的计算公式: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mtable displaystyle="true" columnalign="right left right left right left right left right left right left" columnspacing="0em 2em 0em 2em 0em 2em 0em 2em 0em 2em 0em" rowspacing="3pt"><mtr><mtd><msub><mi>p</mi><mn>1</mn></msub></mtd><mtd><mi></mi><mo>=</mo><msub><mi>v</mi><mn>2</mn></msub><msub><mi>w</mi><mn>3</mn></msub><mo>−</mo><msub><mi>v</mi><mn>3</mn></msub><msub><mi>w</mi><mn>2</mn></msub></mtd></mtr><mtr><mtd><msub><mi>p</mi><mn>2</mn></msub></mtd><mtd><mi></mi><mo>=</mo><msub><mi>v</mi><mn>3</mn></msub><msub><mi>w</mi><mn>1</mn></msub><mo>−</mo><msub><mi>v</mi><mn>1</mn></msub><msub><mi>w</mi><mn>3</mn></msub></mtd></mtr><mtr><mtd><msub><mi>p</mi><mn>3</mn></msub></mtd><mtd><mi></mi><mo>=</mo><msub><mi>v</mi><mn>1</mn></msub><msub><mi>w</mi><mn>2</mn></msub><mo>−</mo><msub><mi>v</mi><mn>2</mn></msub><msub><mi>w</mi><mn>1</mn></msub></mtd></mtr></mtable></math> 线代本质#5:点积(数量积)叉积(向量积)与其几何理解(向量点积、叉积) https://bluish.net/archives/2318/ 作者 bluish 发布时间 2025-06-30 许可协议 CC BY-SA 4.0 复制版权信息 标签: 线性代数
[...]方向余弦三维空间中的向量(x,y,z),其x的方向余弦为,y、z同理:cosx=x|r|具有性质:① er=1|r|(x,y,z)=1|r|⋅r=单位向量② cos2α+cos2β+cos2γ=1投影向量m于向量n上的投影,即为向量m的切面与向量n的交点m',mm'垂直于向量n。投影的计算:(a→在x上的投影)Prjxa=|a|⋅cosφ数量积公式:|m→|⋅|n→|⋅cosθ(即投影[...]