线代本质#4:矩阵的用途——求解特定线性方程组(矩阵用途、秩、线性方程组) 作者: bluish 时间: 2025-06-27 分类: 未分类 矩阵的用途有描述空间变换、求解特定的线性方程组。 #线性方程组求解 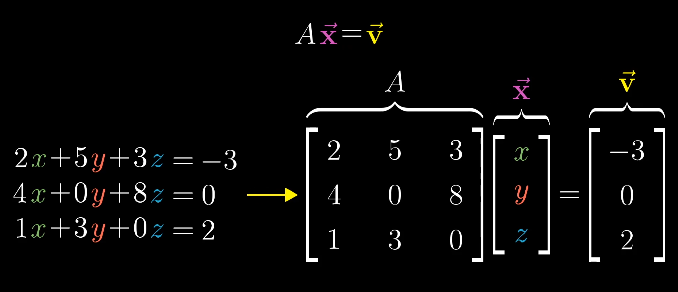 线性方程组可转换为`系数矩阵A×位置向量x=常数向量v` 从几何上看,为向量x通过矩阵A变换为向量v,因此,将向量v通过A的相反变换,即A^-1逆矩阵,即可得出向量x。 即:<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mover><mi>x</mi><mo stretchy="false">→</mo></mover></mrow><mo>=</mo><mrow><mover><mi>v</mi><mo stretchy="false">→</mo></mover></mrow><mo>∗</mo><msup><mi>A</mi><mrow><mo>−</mo><mn>1</mn></mrow></msup></math> #特殊的系数矩阵 若det(A)=0,则空间被压缩为一个点,一条直线或一个平面(三维),此时: 1. 逆矩阵不存在,因函数无法做到将低维转换为高维 2. 解仍可能存在,如“线”的情况下向量v恰巧在同一条线上。 #矩阵的秩 矩阵的秩用于描述变换矩阵自身的情况。 矩阵带给向量的所有可能的变换结果的集合(见下式),即为矩阵的列空间。 <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mi>A</mi><mo>∗</mo><mrow><mover><mi>x</mi><mo stretchy="false">→</mo></mover></mrow></math> 因为矩阵带给向量的所有可能变换结果,均由矩阵变换后的基向量(即矩阵中的列)所组成,即变换后基向量所张成的空间,所以此集合成为矩阵的列空间。 因此,**秩即是列空间的维数。** 如果列空间的维(即基向量的张成空间)与输入空间的维数相等,则矩阵满秩。 如3×2矩阵,列空间二维,输入空间二维,满秩;非共线性3×3矩阵,列空间为三维,输入空间为三维,满秩;双重共线性3×3矩阵,列空间二维,输入空间为三维,秩为2. 线代本质#4:矩阵的用途——求解特定线性方程组(矩阵用途、秩、线性方程组) https://bluish.net/archives/2314/ 作者 bluish 发布时间 2025-06-27 许可协议 CC BY-SA 4.0 复制版权信息 标签: 线性代数