线代本质#3:行列式——线性变换的缩放比例(行列式、矩阵缩放) 作者: bluish 时间: 2025-06-27 分类: 未分类 #行列式的含义 行列式的含义为**线性变换(矩阵)带来的缩放比例,即线性变换对面积(二维)/体积(三维)产生改变的比例。**  如图,经矩阵变换后,原一单位基围成的面积1,被缩放为平行四边形,面积变为3×2=6。 如果行列式为0,则代表矩阵的列必然存在线性相关;二维中将变为直线或点,三维中将变成平面、直线或点。 #负值行列式 负值行列式代表空间取向发生翻转,从几何(二维)上看,ihat与jhat的左右关系发生调转(从一周考虑)。 可以理解为在空间翻转的过程中,行列式的值逐渐减小,在越过0(二维中即共线)之后,空间翻转,变为负值。 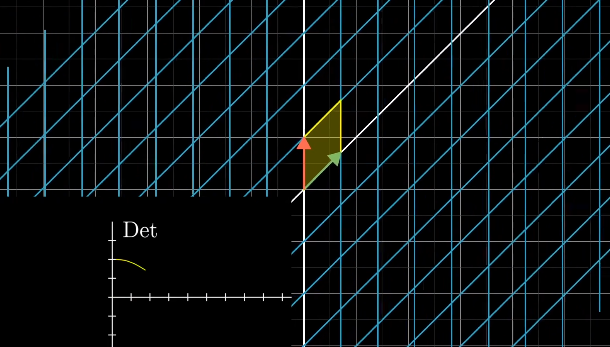 行列式为正,ihat位于jhat右侧 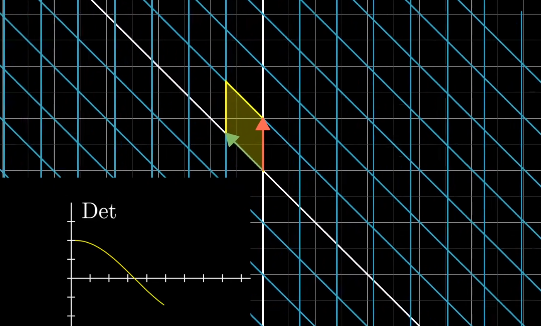 行列式为负,ihat位于jhat左侧 对于三维,我们可以通过右手判断空间是否翻转。如果变换后无法使用右手的三手指相对关系进行比拟,变为左手法则,则证明空间反转。 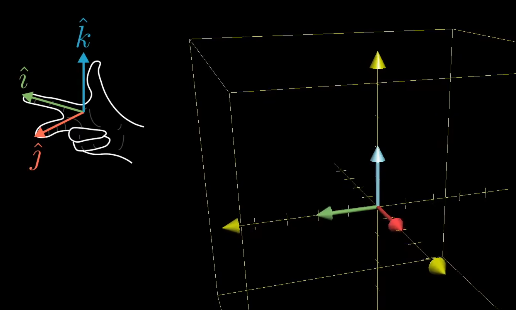 #行列式的计算 行列式的公式: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mi>D</mi><mi>e</mi><mi>t</mi><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">(</mo><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">[</mo><mtable columnspacing="1em" rowspacing="4pt"><mtr><mtd><mi>a</mi></mtd><mtd><mi>b</mi></mtd></mtr><mtr><mtd><mi>c</mi></mtd><mtd><mi>d</mi></mtd></mtr></mtable><mo data-mjx-texclass="CLOSE">]</mo></mrow><mo data-mjx-texclass="CLOSE">)</mo></mrow><mo>=</mo><mi>a</mi><mi>d</mi><mo>−</mo><mi>b</mi><mi>c</mi></math> 若将c、b视为0,则矩阵变换后为平行四边形(变换后一单位基为(a,0),(0,d)),面积为底(a)×高(d),即ad。所以,可将c、b视为**平行四边形在对角方向上拉伸或压缩了多少**。因此行列式的值为ad-cb。 从几何面积上计算验证: 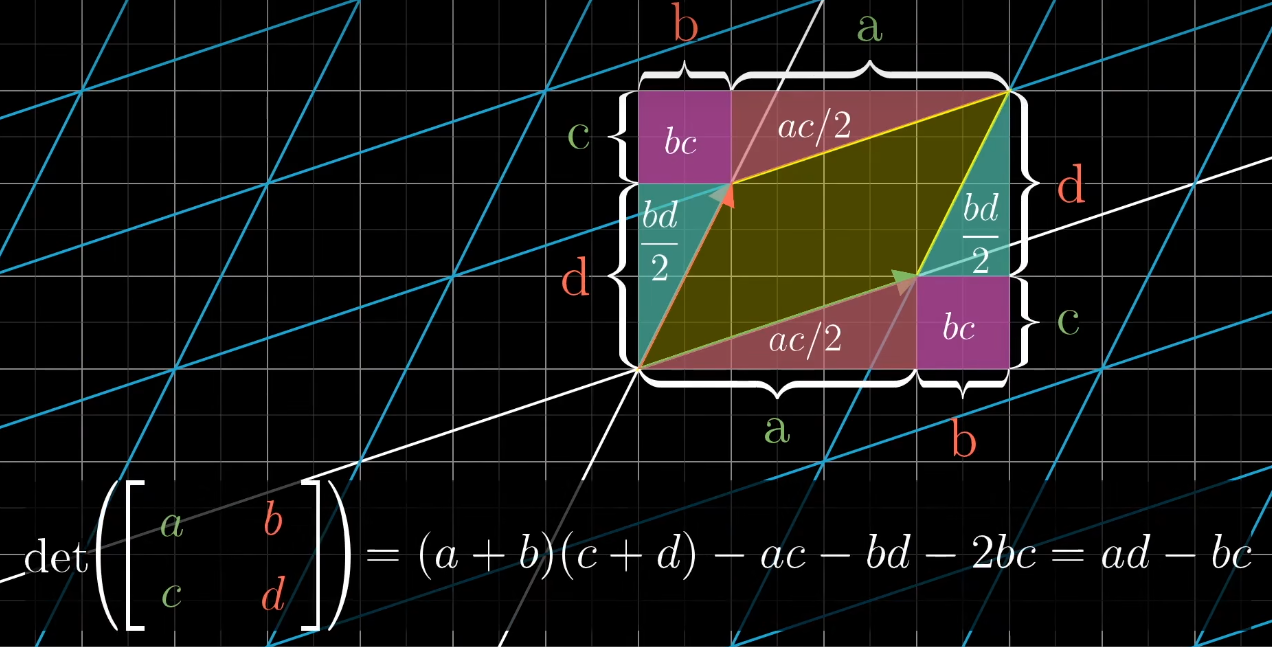 ##计算的性质 Det(M1M2)=Det(M1)Det(M2) 行列式表示体积缩放,复合变换的总体积变化就是缩放因子的连乘。 线代本质#3:行列式——线性变换的缩放比例(行列式、矩阵缩放) https://bluish.net/archives/2305/ 作者 bluish 发布时间 2025-06-27 许可协议 CC BY-SA 4.0 复制版权信息 标签: 线性代数