线代本质#6:向量夹角、投影、正交(向量夹角、向量投影、正交向量/矩阵) 作者: bluish 时间: 2025-06-30 分类: 未分类 xian带#方向余弦 三维空间中的向量(x,y,z),其x的方向余弦为,y、z同理: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mi>cos</mi><mo data-mjx-texclass="NONE"></mo><mi>x</mi><mo>=</mo><mfrac><mi>x</mi><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mi>r</mi><mo data-mjx-texclass="CLOSE">|</mo></mrow></mfrac></math> 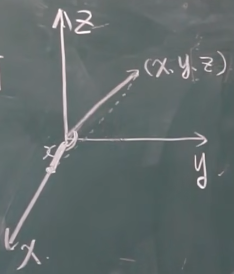 具有性质: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msub><mi>① e</mi><mrow><mi>r</mi></mrow></msub><mo>=</mo><mfrac><mn>1</mn><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mi>r</mi><mo data-mjx-texclass="CLOSE">|</mo></mrow></mfrac><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">(</mo><mi>x</mi><mo>,</mo><mi>y</mi><mo>,</mo><mi>z</mi><mo data-mjx-texclass="CLOSE">)</mo></mrow><mo>=</mo><mfrac><mn>1</mn><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mi>r</mi><mo data-mjx-texclass="CLOSE">|</mo></mrow></mfrac><mo>⋅</mo><mi>r</mi><mo>=单位向量</mo></math> <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msup><mi>② cos</mi><mrow><mn>2</mn></mrow></msup><mo data-mjx-texclass="NONE"></mo><mi>α</mi><mo>+</mo><msup><mi>cos</mi><mrow><mn>2</mn></mrow></msup><mo data-mjx-texclass="NONE"></mo><mi>β</mi><mo>+</mo><msup><mi>cos</mi><mrow><mn>2</mn></mrow></msup><mo data-mjx-texclass="NONE"></mo><mi>γ</mi><mo>=</mo><mn>1</mn></math> #投影 向量m于向量n上的投影,即为向量m的切面与向量n的交点m',mm'垂直于向量n。 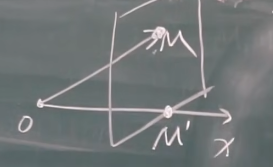 投影的计算: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mo>(</mo><mrow><mover><mi>a</mi><mo stretchy="false">→</mo></mover></mrow><mo>在</mo><mi>x</mi><mo>上的投影)</mo><mi>P</mi><mi>r</mi><msub><mi>j</mi><mrow><mi>x</mi></mrow></msub><mi>a</mi><mo>=</mo><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mi>a</mi><mo data-mjx-texclass="CLOSE">|</mo></mrow><mo>⋅</mo><mi>cos</mi><mo data-mjx-texclass="NONE"></mo><mi>φ</mi></math> #数量积 公式: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mrow><mover><mi>m</mi><mo stretchy="false">→</mo></mover></mrow><mo data-mjx-texclass="CLOSE">|</mo></mrow><mo>⋅</mo><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mrow><mover><mi>n</mi><mo stretchy="false">→</mo></mover></mrow><mo data-mjx-texclass="CLOSE">|</mo></mrow><mo>⋅</mo><mi>cos</mi><mo data-mjx-texclass="NONE"></mo><mi>θ(即投影乘以底向量的模)</mi></math> 或 <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><msub><mi>x</mi><mrow><mn>1</mn></mrow></msub><msub><mi>x</mi><mrow><mn>2</mn></mrow></msub><mo>+</mo><msub><mi>y</mi><mrow><mn>1</mn></mrow></msub><msub><mi>y</mi><mrow><mn>2</mn></mrow></msub></math> 更多请见文章——[线性代数#5:点积(数量积)叉积(向量积)的几何含义](https://bluish.net/archives/2318/ "线性代数#5:点积(数量积)叉积(向量积)的几何含义") #向量之间的夹角 因为由数量积公式ab=|a||b|×cosθ,所以: <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mi>cos</mi><mo data-mjx-texclass="NONE"></mo><mi>θ</mi><mo>=</mo><mfrac><mrow><mi>a</mi><mo>⋅</mo><mi>b</mi></mrow><mrow><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mi>a</mi><mo data-mjx-texclass="CLOSE">|</mo></mrow><mo>⋅</mo><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mi>b</mi><mo data-mjx-texclass="CLOSE">|</mo></mrow></mrow></mfrac><mo>(用数量积公式</mo><mn>2</mn><mo>计算</mo><mi>a</mi><mo>·</mo><mi>b</mi><mo>)</mo></math> #向量之间的投影长度 <math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mi>P</mi><mi>r</mi><msub><mi>j</mi><mrow><mo>底</mo></mrow></msub><mo>投=</mo><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">|</mo><mo>投影向量</mo><mo data-mjx-texclass="CLOSE">|</mo></mrow><mo>⋅</mo><mi>cos</mi><mo data-mjx-texclass="NONE"></mo><mi>θ(利用“向量间的夹角”得cosθ)</mi></math> #正交 **正交即为垂直。** 两向量a、b,若(a,b)=0(即点积为0),则两向量正交,a⊥b。 两两正交的非零向量组称为正交向量组,必线性无关。 ##正交矩阵 普通的可逆矩阵满足A·B=E(单位矩阵),此处B即为A逆。 对于正交矩阵(一个特殊矩阵),它有**“行列向量两两正交且单位长度”的特殊结构**[因],因此**它的转置矩阵在此结构下恰为它的逆变换**[果1],即转置矩阵为它的逆矩阵,所以此时A·A转置=E。 几何上,正交矩阵对应的线性变换**不会改变向量的长度或方向之间的夹角,仅表示旋转或翻转**[果2]等“刚性变换”。 线代本质#6:向量夹角、投影、正交(向量夹角、向量投影、正交向量/矩阵) http://bluish.net/archives/2323/ 作者 bluish 发布时间 2025-06-30 许可协议 CC BY-SA 4.0 复制版权信息 标签: 线性代数